An Empirical Study of Overlapping Rotor Interference for a Small Unmanned Aircraft Propulsion System
[...]
Test results (
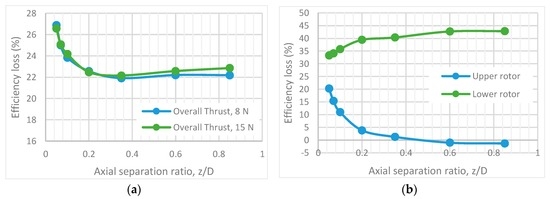
Figure 15a) indicate that co-axial system performance is highest when the rotors are operating in a region z/D > 0.25. At that region the performance loss was recorded to be approximately 22% which is close to the values predicted by the momentum theory. It could be stated also that in this particular setup, with highly-twisted rotors, the performance gains are seen up until z/D = 0.25. Measurements show little to no variation in performance at two distinctively different net thrust magnitudes. Some variation is noticeable when z/D > 0.35, however, due to the test rig induced error, small differences should not be treated as efficiency gains/losses. Some of the data deviation from linearity could be linked to the drag force produced by the lower motor and torque sensor assembly interaction with the upper rotor slipstream; further investigation in this region is needed.
[...]
[...]
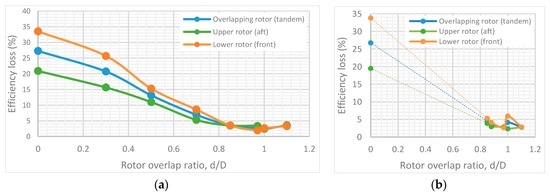
Figure 18. Overlapping rotor (tandem) performance in terms of percentage efficiency loss over two isolated rotors (z/D = 0.05): (
a) overall thrust = 8 N; and (
b) overall thrust = 15 N.
The rotor tested in this study has fixed pitch. As such, the angular synchronization of the rotors is not possible due to the requirement for torque balance, therefore, the desired z/D = 0 could not be achieved. The test results presented in
Figure 17 were completed at the lowest possible z/D = 0.05. All of the gathered data was compared to the momentum theory using the derived overlap interference factor kov
. Two cases of momentum theory where compared to the test results—rotors were assumed to operate at the same plane and that the lower rotor is operating in the fully developed upper rotor slipstream (detailed derivation of all momentum theory cases can be found in [
31]). Harris [
32] derived overlap interference factors for the full range of d/D ratios, which were also used to compare the empirical results. Overlapping rotor, kov was calculated from the gathered data by:
kov=Pu (measured)+Pl (measured)2Pisolated (single)
(8)
where the isolated power is obtained from single rotor tests, using half of the total power measured in overlapping rotor tests.
Test results show that at z/D = 0.05 in the region 1 < d/D < 1.1 (fully-separated rotors) both rotors perform slightly worse than two isolated rotors. In comparison to the co-axial setup, where the lower rotor is operating at a worse efficiency with regards to the upper rotor at any tested setup condition, the partially overlapping tests showed that, in some cases, the lower rotor can outperform the upper rotor. The lower and upper rotor in a partially overlapped system switch their performances at approximately 0.95 < d/D < 1, in the tested overall thrust condition 8 N (
Figure 17a). At the higher system thrust of 15 N (
Figure 17b) the lower rotor does not manage to outperform the upper one, however their performance almost matches. Similar results were observed by Ramasamy [
15] when testing untwisted rotors. Observations by Ramasamy [
15] show a much more distinct performance transition between the upper and lower rotor at d/D > 0.8. However, for highly-twisted rotors the performance switch was seen at d/D = 0.5. In both cases test results did not show any switch back past d/D = 1. It must be noted that Ramasamy’s [
15] tests were done at a much higher overall thrust of approximately 72 N. These contradictory results with a possible link to the system thrust requires further analysis using rotor flow fields.
As observed in
Figure 18, the overall system has an approximately 25% change in performance through the tested d/D range in comparison to two isolated rotors. The smallest efficiency loss (~3%), at both tested thrust conditions at z/D = 0.05 can be observed in the region close to the full rotor separation of d/D = 1. However, at the higher thrust settings d/D = 1 has more pronounced efficiency drop (~4%) when compared to the lower thrust test. This could be possibly explained by the increase of the energy in the rotor tip vortices. The same trends can be seen when looking at the thrust and power-sharing conditions of the upper and lower rotors through the tested d/D range (
Figure 19). When d/D < 1, with the decrease of the rotor overlap ratio there is an increase in the lower rotor thrust output and decrease in the lower rotor induced power. Both slopes meet at approximately d/D > 0.9, meaning that both rotors start performing at similar efficiency.
6. Conclusions
This paper has attempted to bring some clarity to small UAV overlapping rotor propulsion system design and performance when off-the-shelf rotors are used. The off-the-shelf T-Motor 16 inch × 5.4 inch rotor, which has diameter of 0.4064 m and a fixed pitch of 9.5 degrees (measured at 75% span), was scanned and digitally reconstructed giving a better understanding of the airfoil shapes, chord distribution, and individual section angles of incidence. A unique semi-automatic test rig was designed and manufactured to give a flexible platform with which single and overlapping rotor propulsion systems could be tested. To support empirical single rotor and overlapping rotor test results, the rotor profile drag data was obtained using blade element momentum theory. In summary, the following observations were made:
- A high quality small UAV off-the-shelf rotor has been measured to have a zero lift drag coefficient, Cd0
- = 0.019.
- A thrust sharing change of 21% was measured over the tested axial separation distances 0.05 < z/D < 0.85, when fixed pitch rotors were operated in the torque-balanced setup. The upper rotor produced more thrust than the lower at any tested z/D ratio.
- Highly-twisted small UAV rotors in a conventional torque-balanced co-axial configuration are 22% less efficient when compared to two isolated rotors whose combined solidity is equal to that of a co-axial system. Momentum theory predicts a 26% increase in the induced power for torque-balanced co-axial rotor setups. The rotor axial separation from z/D > 0.25 had no effect on the overall system performance. The lowest performance figure of 26% loss over two isolated rotors was observed at z/D = 0.05.
- When comparing upper and lower rotors in a co-axial torque-balanced setup, it has been observed that the upper rotor operates at a higher efficiency than the lower rotor throughout the tested 0.05 < z/D < 0.85 range. Interference of the upper to the lower rotor was apparent throughout 0.05 < z/D < 0.85. Lower to upper rotor interference was observed only at 0.05 < z/D < 0.6 and the peak decrease the upper rotor efficiency was observed to be 21%. On the other hand, the lower rotor efficiency increased by 10% over the same axial separation range (0.05 < z/D < 0.6). These upper and lower rotor performance deviations affected the overall performance of the system at z/D < 0.25.
- The upper and lower rotors were compared to a single isolated rotor’s performance when operating in a co-axial torque balanced setup. At the range of axial separation of z/D > 0.6 the upper rotor operates at a similar performance to that observed on a single isolated rotor. In contrast, the lower rotor at the same axial separation range experiences an efficiency loss of 42%, which decreased to 33% at z/D = 0.05.
- Swirl recovery effects were observed in the overall co-axial rotor performance by running two co-rotating rotors in a co-axial setup, when the upper and lower rotor torque was equal. The results were compared to the conventional co-axial setup running rotors in the torque-balanced mode. Overall, the conventional co-axial rotor system was measured to be approximately 4% more efficient throughout all tested axial ratios 0.05 < z/D < 0.85, revealing the magnitude of the swirl recovery contribution to the overall system performance.
- Swirl recovery effects were observed on the individual upper and lower co-axial rotor performance by running two co-rotating rotors in a co-axial setup when the upper and lower rotor torque was equal. This was then compared to the results of a conventional co-axial setup running rotors in the torque-balanced mode. The lower rotor in a co-axial co-rotating system runs approximately 4% less efficiently throughout all tested axial separations 0.05 < z/D < 0.85. No differences in upper rotor performance were detected. These measurements have revealed that swirl recovery has little to no effect on the upper rotor and all of the efficiency gains are linked to the lower rotor.
- The performance of a partially-overlapped (tandem) multi-rotor system, in a torque-balanced setup, was tested at an axial separation ratio z/D = 0.05 and the results were compared to two isolated rotors. The overall efficiency of the system increased through the overlap range of 0 < d/D < 1. The efficiency of the system started to decrease again at d/D > 1. The peak efficiency of the system was observed at d/D = 0.97, but was approximately 3% less efficient when compared to the performance of two isolated rotors.
- Performance of the upper (aft) rotor of a partially-overlapped torque-balanced system tested at z/D = 0.05 was better than the lower (front) rotor, up to d/D > 0.95. The lower rotor was observed to operate at a slightly higher efficiency in the region 0.95 < d/D < 1 at an overall thrust of 8 N. At a higher overall thrust of 15 N, such a performance change was not present. Dependencies on the overall thrust were recorded at d/D = 1 also, and with the increase of thrust the lower rotor performance decreased.
- Dependencies on the axial separation ratio z/D when rotors are operating in partial overlap of d/D = 0.85 at a torque-balanced state were recorded. Through the tested axial separation range of 0.05 < z/D < 0.85, approximately a 2% increase in overall performance was recorded. Most of the gains occurred at z/D < 0.35.
[...]
Sehr Interessantes Papier, einige Aspekte wie unterschiedliche Propeller Größen und verschiedene Propeller Pitches sind leider nicht aufgenommen, aber zumindest liefert es eine gute Richtung.
Die Performance eines Koxial Systems ist am besten, wenn z/D bei 0.25 bis max 0.35 liegt.
Die Performance eines Koxial Systems wird mit steigender Rotor Overlap Ratio d/D besser, bis das maximum bei 1.1 bei nicht mehr überlappenden Antrieben den Höhepunkt erreicht.
So versuche ich jetzt, das mein Setup die z/D Ratio von 0.25 erreicht. Die overlap Ratio werde ich von Null (komplett überlappend) auf ca 0.25 (etwas versetzt) anheben.
Vielleicht hilft euch das auch.